YOĞUNLUK

Suda çözünmeyen katı maddelerin bazıları suda yüzer, bazıları suda batar. Bir maddenin suda yüzme veya batma durumunu açıklamak için, yoğunluk kavramı kullanılır. Suda yüzen maddelerin yoğunluğu suyun yoğunluğundan küçük, batan maddelerin yoğunluğu suyun yoğunluğundan büyüktür.

Bir maddenin birim hacminin (1 cm³) kütlesine maddenin yoğunluğu denir. Yoğunluk maddenin ayırt edici özelliklerinden biridir.

Bir maddenin yoğunluğunu hesaplayabilmek için kütlesinin ve hacminin bilinmesi gerekir. Bir maddenin kütlesinin hacmine oranı o maddenin yoğunluğunu verir. Yoğunluk kısaca d harfi ile gösterilirken, kütle m ve hacim V harfi ile gösterilir. Kütlenin birimi gram ve hacmin birimi cm³ olarak alındığından yoğunluğun birimi g/cm³ olarak bulunur. Bir maddenin yoğunluğunu bulmak için aşağıdaki eşitliği kullanırız.

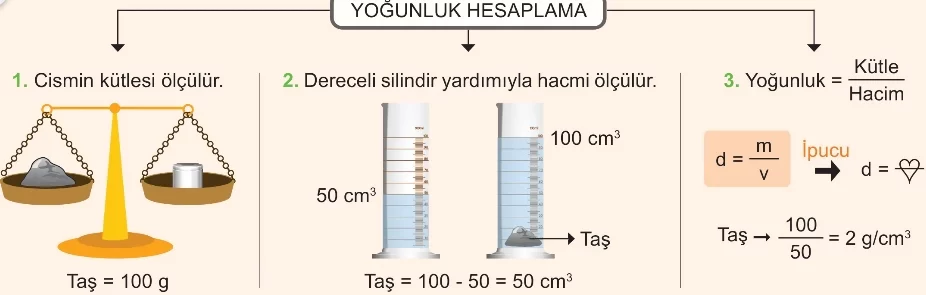
Katı maddelerin yoğunluğunu hesaplamak için kütlelerinin ve hacimlerinin bilinmesi gerekir. Örneğin, bir taş parçasının yoğunluğunun hesaplanabilmesi için önce kütlesi terazi ile ölçülür. Daha sonra aynı taş parçasının hacmi dereceli silindire biraz su koyulduktan sonra, taş parçası bu dereceli silindirin içine bırakılarak ölçülür.

Suya bırakılan taş parçasının hacmi; taş parçası suya bırakıldıktan sonra dereceli silindirde ölçülen değer ile taş parçası suya bırakılmadan önce dereceli silindirde ölçülen değer arasındaki farka eşittir.

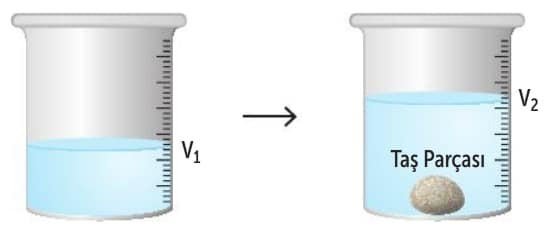
Taş parçasının yoğunluğu; kütlesi, hacmine bölünerek bulunabilir. Aynı taş parçasını eşit olmayan üç parçaya bölüp, her bir parçanın kütlesini ve hacmini ölçtükten sonra, taş parçalarının yoğunluklarını hesapladığımızda sonucun değişmediğini görebiliriz. Bu durum bize aynı maddenin yoğunluğunun değişmediğini gösterir.

Sıvı maddelerin de yoğunluğunu hesaplamak için katı maddeler gibi kütlelerinin ve hacimlerinin bilinmesi gerekir. Örneğin, suyun yoğunluğunun hesaplanabilmesi için kütlesi ve hacminin belirlenmesi gerekir. Bunun için boş bir dereceli silindir terazinin üzerine konur ve darası belirlenir. Daha sonra bu dereceli silindire bir miktar su koyularak terazide brüt kütle ölçülür. Brüt kütle ile dara arasındaki fark suyun kütlesini verir. Dereceli silindir yardımıyla suyun hacmi belirlenir. Suyun yoğunluğu; kütlesi, hacmine bölünerek bulunabilir.

Aynı şartlarda farklı maddelerin yoğunlukları birbirinden farklıdır. Aşağıdaki tabloda bazı maddelerin kütleleri, hacimleri ve yoğunlukları verilmiştir.

Maddeler	Kütle (g)	Hacim (cm3)	Yoğunluk (g/cm3)
Su	$100$	$100$	$1$
Altın	$1930$	$100$	$19,3$
Demir	$780$	$100$	$7,8$
Mum	$80$	$100$	$0,8$
Gümüş	$1050$	$100$	$10,5$
Cıva	$1360$	$100$	$13,6$
Alkol	$78$	$100$	$0,78$
Zeytinyağı	$92$	$100$	$0,92$
Mısır Yağı	$93$	$100$	$0,93$
Silgi	$134$	$100$	$1,34$
Buz	$90$	$100$	$0,9$

Birbiri içinde çözünmeyen sıvı maddelerin yoğunluklarını birbiri ile karşılaştırabiliriz. Yoğunlukları farklı olan ve birbiri içinde çözünmeyen sıvılar aynı kap içine koyuldukları zaman yoğunluklarının büyüklüğüne göre sıralanırlar.

Bir kaba birbiriyle karışmayan ikiden fazla sıvı koyulduğunda, sıvılar yoğunluğu azalacak şekilde aşağıdan yukarıya doğru sıralanırlar. Yoğunluğu büyük olan sıvı en altta kalırken, yoğunluğu en az olan sıvı en üstte kalır. Yoğunluğu bu iki sıvının arasında olan sıvı ise arada bir yerde kalır.

Kütle – Yoğunluk – Hacim İlişkisi

Cisimlerin Yüzme – Askıda Kalma – Batma Durumu

• Bir sıvı içerisine yoğunluğu sıvının yoğunluğundan daha büyük bir cisim bırakıldığında, cisim batar.
• Bir sıvı içerisine yoğunluğu sıvının yoğunluğuna eşit bir cisim bırakıldığında, cisim askıda kalır.
• Bir sıvı içerisine yoğunluğu sıvının yoğunluğundan küçük bir cisim bırakıldığında cisim yüzer.
• Birbirine karışmayan sıvılar aynı kap içerisine konulduğunda yoğunluğu fazla olan sıvı kabın dibine çöker, yoğunluğu az olan sıvı kabın üst kısmında kalır.

Maddelerin katı hali, sıvı halinden daha yoğundur. Ancak bu durum buz için geçerli değildir. Buzun yoğunluğu $0,9 \text{ g}/\text{cm}^3$, suyun yoğunluğu $1 \text{ g}/\text{cm}^3$‘tür. Bu yüzden göllerin kışı üst kısmı buz tutarken alt kısımda yaşam devam eder.

SUYUN YOĞUNLUĞU VE CANLILAR İÇİN ÖNEMİ

Sıvı hâlden katı hâle geçen maddelerin hacmi azalır, yoğunluğu artar. Su, bu maddelerin dışındadır. Su donduğunda suyun hacmi artar, yoğunluğu azalır. Buzun yoğunluğu suyun yoğunluğundan az olduğu için su içine atılan buz suda yüzer. Saf suyun yoğunluğu 4^oC sıcaklıkta 1 g/cm3 iken buzun yoğunluğu 0,9 g/cm³‘tür.

Buzun yoğunluğunun suyun yoğunluğundan az olması ve buzun suda yüzmesi canlılar için çok önemlidir. Kış mevsiminde donan su, nehir ve göllerin yüzeyini kaplar. Böylece suların dibe doğru donması önlenir. Bu durum sulardaki yaşamın devam etmesini sağlar. Çünkü buzun su üstünde yüzmesiyle denizlerin ve göllerin dipleri uygun sıcaklıkta kalır.

Su dışındaki sıvı maddeler katı hâle geçtiğinde hacimleri küçülür, yoğunlukları büyür. Örneğin zeytinyağı katı hâle geçtiğinde kendi sıvısı içinde batar.

Yoğunluk Çözümlü Örnek Test Soruları

1. Soru

Bir maddenin yoğunluğunu hesaplayabilmek için aşağıdaki niceliklerden hangilerinin bilinmesi zorunludur?

A) Sadece kütlesi

B) Sadece hacmi

C) Kütlesi ve birim hacmi

D) Kütlesi ve hacmi

Cevap: D

Çözüm:

Yoğunluk, bir maddenin birim hacminin kütlesi olarak tanımlanır. Yoğunluk formülü $d = m/V$ olduğu için, yoğunluğun hesaplanabilmesi için maddenin kütlesi ($m$) ve hacmi ($V$) değerlerinin bilinmesi zorunludur.

---

2. Soru

Aynı sıcaklıkta ve ortamda bulunan X, Y ve Z saf maddelerinin yoğunlukları sırasıyla $d_X = 5 \text{ g}/\text{cm}^3$, $d_Y = 1 \text{ g}/\text{cm}^3$ ve $d_Z = 0.8 \text{ g}/\text{cm}^3$‘tür.

Bu maddeler yoğunluğu $1.2 \text{ g}/\text{cm}^3$ olan bir sıvı içerisine bırakıldığında, hangi madde kesinlikle sıvı içinde yüzer?

A) X

B) Y

C) Z

D) Hiçbiri

Cevap: C

Çözüm:

• Bir cismin sıvı içinde yüzebilmesi için, cismin yoğunluğunun sıvının yoğunluğundan küçük olması gerekir ($d_{\text{cisim}} < d_{\text{sıvı}}$).

• Sıvının yoğunluğu: $1.2 \text{ g}/\text{cm}^3$.

• X maddesi: $5 \text{ g}/\text{cm}^3 > 1.2 \text{ g}/\text{cm}^3$ (Batar)

• Y maddesi: $1 \text{ g}/\text{cm}^3 < 1.2 \text{ g}/\text{cm}^3$ (Yüzer veya askıda kalır. Yoğunluk küçük olduğu için yüzer.)

• Z maddesi: $0.8 \text{ g}/\text{cm}^3 < 1.2 \text{ g}/\text{cm}^3$ (Yoğunluk en küçük olduğu için kesinlikle yüzer ve en üstte kalır.)

En küçük yoğunluğa sahip olan Z, sıvı içinde en üstte kalacak şekilde yüzer.

---

3. Soru

Bir demir bilyenin kütlesi eşit kollu terazi ile $78 \text{ g}$ olarak ölçülmüştür. Bu bilyenin hacmi, dereceli silindirde $10 \text{ cm}^3$ olarak bulunmuştur.

Buna göre, demir bilyenin yoğunluğu kaç $\text{g}/\text{cm}^3$‘tür?

A) $0.78$

B) $7.8$

C) $78$

D) $780$

Cevap: B

Çözüm:

Yoğunluk ($d$), kütle ($m$) bölü hacim ($V$) formülüyle hesaplanır:

 

 

Verilenler: $m = 78 \text{ g}$, $V = 10 \text{ cm}^3$.

 

---

4. Soru

Yoğunluk ile ilgili verilen,

I. Maddeler için ayırt edici bir özelliktir.

II. Maddenin kütlesi arttıkça yoğunluğu da artar.

III. Birimi sadece $\text{g}/\text{cm}^3$ tür.

ifadelerinden hangileri doğrudur?

A) Yalnız I

B) I ve II

C) I ve III

D) II ve III

Cevap: A

Çözüm:

• I. Doğru. Yoğunluk, saf maddeleri birbirinden ayırt etmede kullanılır.

• II. Yanlış. Bir maddenin kütlesi veya hacmi artsa da, sıcaklık ve basınç değişmediği sürece yoğunluğu değişmez (sabit kalır).

• III. Yanlış. Birimi $\text{g}/\text{cm}^3$ olabileceği gibi $\text{kg}/\text{m}^3$ veya $\text{kg}/\text{L}$ gibi farklı birimler de kullanılabilir.

---

5. Soru

Grafikte verilen kütle-hacim ilişkisine göre, bu saf madde ile ilgili yoğunluk-kütle grafiği aşağıdakilerden hangisidir?

A) B) C) D)

Cevap: C

Çözüm:

Yoğunluk, madde miktarına (kütle veya hacme) bağlı olarak değişmez. Grafikte kütle artsa bile, maddenin yoğunluğu hep sabit kalmalıdır. Bu durumu en iyi gösteren grafik, kütle eksenine paralel sabit bir çizgi olan C seçeneğidir.

---

6. Soru

Aşağıdaki durumlardan hangisi, maddenin katı halinin sıvı halinden daha az yoğun olmasına bir örnektir?

A) Yağmur yağması

B) Suda yüzen odun parçası

C) Bir sıvı yağın su üzerinde kalması

D) Kışın göl sularının yüzeyden donmaya başlaması

Cevap: D

Çözüm:

• Normalde maddelerin katı hali sıvı halinden daha yoğundur (Bu yüzden katı demir sıvı demirde batar).

• Su, bu kuralın istisnasıdır. Buz (katı su), sıvı sudan daha az yoğundur ($\text{d}_{\text{buz}} \approx 0.9 \text{ g}/\text{cm}^3$, $\text{d}_{\text{su}} \approx 1 \text{ g}/\text{cm}^3$).

• Kışın göl sularının yüzeyden donması ve oluşan buzun su üzerinde kalması, buzun sudan daha az yoğun olmasının sonucudur.

---

7. Soru

Birbirine karışmayan K, L ve M sıvıları aynı kap içine konulduğunda aşağıdaki görünüm elde ediliyor.

Buna göre sıvıların yoğunlukları arasındaki ilişki nasıldır?

A) $d_K > d_L > d_M$

B) $d_M > d_L > d_K$

C) $d_L > d_M > d_K$

D) $d_K = d_L = d_M$

Cevap: B

Çözüm:

Birbirine karışmayan sıvılar aynı kap içine konulduğunda, yoğunluğu en fazla olan sıvı kabın dibinde (en altta) kalır, yoğunluğu en az olan sıvı ise en üstte yer alır.

• En altta: M

• Ortada: L

• En üstte: K

Bu durumda yoğunluk sıralaması: $d_M > d_L > d_K$ şeklinde olmalıdır.