Soru Çözümü
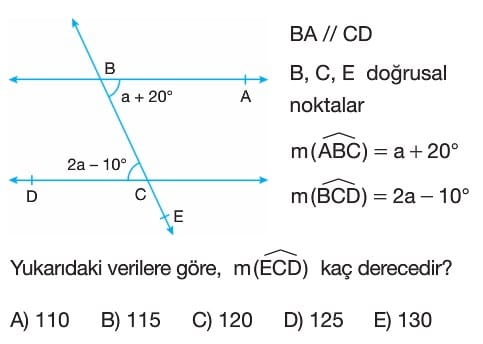
- `BA // CD` olduğundan, şekildeki açılar iç ters açılar olarak kabul edilir ve bu nedenle `m(ABC)` ile `m(BCD)` açıları birbirine eşittir.
- Denklemi kuralım: `$a + 20 = 2a - 10$`.
- Denklemi çözerek `a` değerini bulalım: `$a = 30$`.
- `m(BCD)` açısını hesaplayalım: `$m(BCD) = 2a - 10 = 2(30) - 10 = 60 - 10 = 50°$`.
- `B, C, E` noktaları doğrusal olduğu için `m(BCD)` ve `m(ECD)` açıları bütünler açılardır (toplamları $180°$).
- `m(ECD)` açısını hesaplayalım: `$m(ECD) = 180° - m(BCD) = 180° - 50° = 130°$`.
- Doğru Seçenek E'dır.