Soru Çözümü
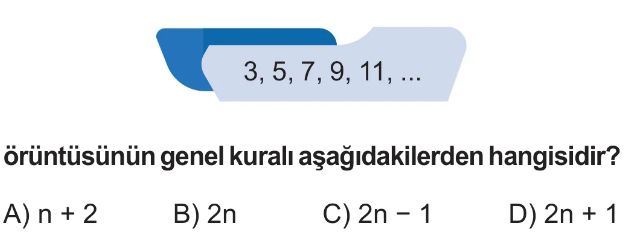
- Verilen örüntü $3, 5, 7, 9, 11, ...$ şeklindedir.
- Örüntüdeki ardışık terimler arasındaki farkı bulalım: $5 - 3 = 2$, $7 - 5 = 2$, $9 - 7 = 2$. Fark sabittir ve $2$'dir.
- Bu sabit fark, genel kuralda $n$ teriminin katsayısını verir. Yani kural $2n$ ile başlamalıdır.
- Şimdi $2n$ ifadesini örüntünün ilk terimi ($n=1$) için deneyelim: $2 \times 1 = 2$. Oysa ilk terim $3$'tür.
- $2$'yi $3$ yapmak için $1$ eklememiz gerekir. Yani kural $2n + 1$ olabilir.
- Bu kuralı diğer terimler için kontrol edelim:
- $n=2$ için: $2 \times 2 + 1 = 4 + 1 = 5$. (Örüntünün ikinci terimi $5$ ile eşleşiyor)
- $n=3$ için: $2 \times 3 + 1 = 6 + 1 = 7$. (Örüntünün üçüncü terimi $7$ ile eşleşiyor)
- $n=4$ için: $2 \times 4 + 1 = 8 + 1 = 9$. (Örüntünün dördüncü terimi $9$ ile eşleşiyor)
- Genel kuralın $2n + 1$ olduğu doğrulanmıştır.
- Doğru Seçenek D'dır.