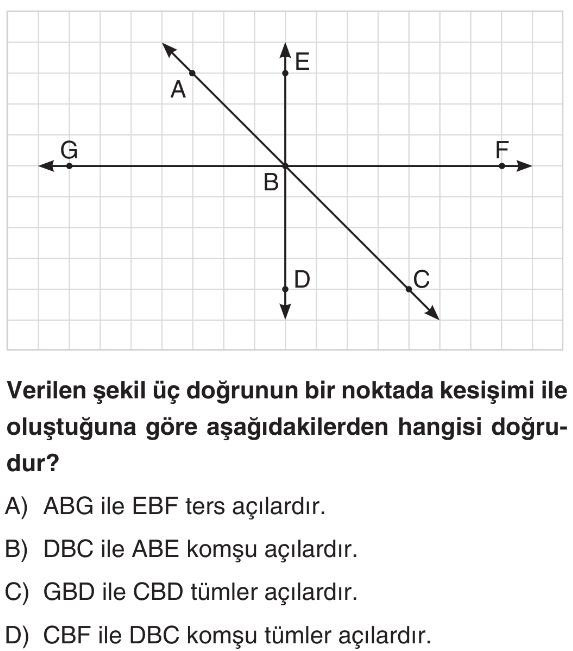
Soru Çözümü
- Şekildeki GF doğrusu ile ED doğrusu, kareli zemine göre birbirine diktir. Bu durumda B noktasında oluşan GBD, DBF, FBE ve EBG açıları $90^\circ$'dir.
- CBF açısı ile DBC açısı, BC ışınını ortak kenar olarak kullanır ve köşeleri B noktasıdır. Bu nedenle bu iki açı komşu açılardır.
- CBF açısı ile DBC açısının toplamı, DBF açısını oluşturur. Yani $m(\angle CBF) + m(\angle DBC) = m(\angle DBF)$ olur.
- Yukarıda belirtildiği gibi DBF açısı $90^\circ$'dir. Dolayısıyla, $m(\angle CBF) + m(\angle DBC) = 90^\circ$ olur.
- Toplamları $90^\circ$ olan açılara tümler açılar denir. Bu durumda CBF ve DBC açıları hem komşu hem de tümler açılardır.
- Doğru Seçenek D'dır.