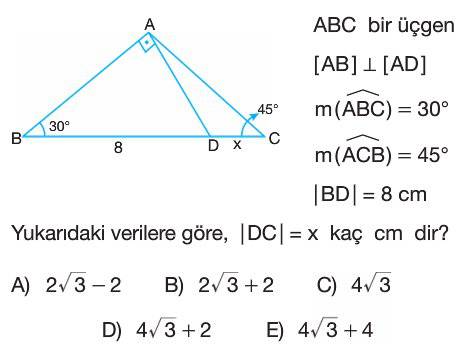
Soru Çözümü
ÇÖZÜM:
- Verilen bilgilere göre, $[AB] \perp [AD]$ olduğundan $\triangle ABD$ bir dik üçgendir ve $m(\widehat{BAD}) = 90^\circ$.
- $\triangle ABD$ dik üçgeninde $m(\widehat{ABD}) = 30^\circ$ ve $m(\widehat{BAD}) = 90^\circ$ olduğu için, $m(\widehat{ADB}) = 180^\circ - (90^\circ + 30^\circ) = 60^\circ$.
- $|BD| = 8$ cm olduğundan, $30^\circ-60^\circ-90^\circ$ üçgen özelliklerini kullanarak $|AD|$ kenarını buluruz: $|AD| = |BD| \cdot \sin(30^\circ) = 8 \cdot \frac{1}{2} = 4$ cm.
- $\triangle ABC$ üçgeninde iç açılar toplamı $180^\circ$ olduğundan, $m(\widehat{BAC}) = 180^\circ - (m(\widehat{ABC}) + m(\widehat{ACB})) = 180^\circ - (30^\circ + 45^\circ) = 105^\circ$.
- $m(\widehat{DAC})$ açısını bulmak için $m(\widehat{BAC}) - m(\widehat{BAD})$ işlemini yaparız: $m(\widehat{DAC}) = 105^\circ - 90^\circ = 15^\circ$.
- $\triangle ADC$ üçgeninde iç açılar toplamı $180^\circ$ olduğundan, $m(\widehat{ADC}) = 180^\circ - (m(\widehat{DAC}) + m(\widehat{ACD})) = 180^\circ - (15^\circ + 45^\circ) = 120^\circ$.
- $\triangle ADC$ üçgeninde Sinüs Teoremi'ni uygularız: $\frac{|AD|}{\sin(m(\widehat{ACD}))} = \frac{|DC|}{\sin(m(\widehat{DAC}))}$.
- Değerleri yerine yazarsak: $\frac{4}{\sin(45^\circ)} = \frac{x}{\sin(15^\circ)}$.
- $\sin(45^\circ) = \frac{\sqrt{2}}{2}$ ve $\sin(15^\circ) = \sin(45^\circ - 30^\circ) = \sin(45^\circ)\cos(30^\circ) - \cos(45^\circ)\sin(30^\circ) = \frac{\sqrt{2}}{2}\frac{\sqrt{3}}{2} - \frac{\sqrt{2}}{2}\frac{1}{2} = \frac{\sqrt{6} - \sqrt{2}}{4}$.
- Denklemi çözelim: $\frac{4}{\frac{\sqrt{2}}{2}} = \frac{x}{\frac{\sqrt{6} - \sqrt{2}}{4}} \Rightarrow \frac{8}{\sqrt{2}} = \frac{4x}{\sqrt{6} - \sqrt{2}}$.
- Paydayı rasyonel yaparak ve sadeleştirerek: $4\sqrt{2} = \frac{4x}{\sqrt{6} - \sqrt{2}}$.
- Her iki tarafı $4$'e bölersek: $\sqrt{2} = \frac{x}{\sqrt{6} - \sqrt{2}}$.
- $x = \sqrt{2}(\sqrt{6} - \sqrt{2}) = \sqrt{12} - \sqrt{4} = 2\sqrt{3} - 2$ cm.
- Doğru Seçenek A'dır.