Soru Çözümü
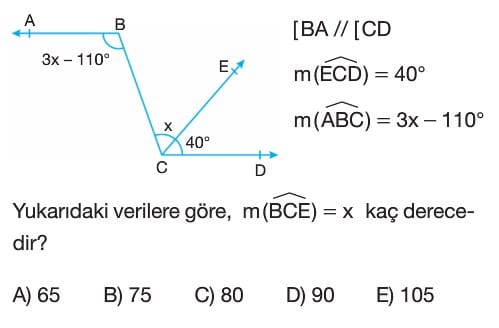
- Verilen bilgilere göre, `[BA // [CD` olduğu belirtilmiştir.
- BC doğrusu bir kesen olarak kabul edildiğinde, `$m(\widehat{ABC})$` ve `$m(\widehat{BCD})$` iç ters açılardır.
- İç ters açılar birbirine eşit olduğundan, `$m(\widehat{ABC}) = m(\widehat{BCD})$`.
- Şekilde görüldüğü gibi, `$m(\widehat{BCD})$` açısı `$m(\widehat{BCE})$` ve `$m(\widehat{ECD})$` açılarının toplamına eşittir. Yani, `$m(\widehat{BCD}) = m(\widehat{BCE}) + m(\widehat{ECD})$`.
- Verilen açı değerlerini bu eşitlikte yerine yazarsak: `$3x - 110^\circ = x + 40^\circ$`.
- Denklemi çözmek için terimleri düzenleyelim: `$3x - x = 40^\circ + 110^\circ$`.
- Bu durumda, `$2x = 150^\circ$` elde edilir.
- Her iki tarafı 2'ye bölerek `$x$` değerini buluruz: `$x = 75^\circ$`.
- Doğru Seçenek B'dır.