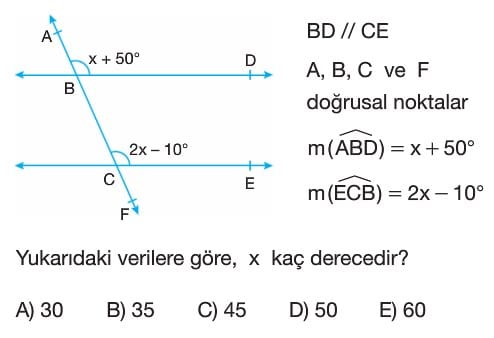
Soru Çözümü
- Verilen bilgilere göre, $BD // CE$ ve $A, B, C, F$ noktaları doğrusaldır.
- Açı $m(\widehat{ABD}) = x + 50^\circ$ ve $m(\widehat{ECB}) = 2x - 10^\circ$ olarak verilmiştir.
- $A, B, F$ noktaları doğrusal olduğundan, $m(\widehat{ABD})$ ve $m(\widehat{DBF})$ bütünler açılardır (doğru açı oluştururlar).
- Bu durumda, $m(\widehat{DBF}) = 180^\circ - m(\widehat{ABD}) = 180^\circ - (x + 50^\circ)$ olur.
- $BD // CE$ olduğundan, $m(\widehat{DBF})$ ve $m(\widehat{ECB})$ açıları karşı durumlu açılardır (iç ters açılar değil, aynı taraftaki iç açılar).
- Karşı durumlu açıların toplamı $180^\circ$'dir. Yani, $m(\widehat{DBF}) + m(\widehat{ECB}) = 180^\circ$.
- Denklemi kuralım: $(180^\circ - (x + 50^\circ)) + (2x - 10^\circ) = 180^\circ$.
- Denklemi çözelim: $180^\circ - x - 50^\circ + 2x - 10^\circ = 180^\circ$.
- $x + 120^\circ = 180^\circ$.
- $x = 180^\circ - 120^\circ$.
- $x = 60^\circ$.
- Doğru Seçenek E'dır.