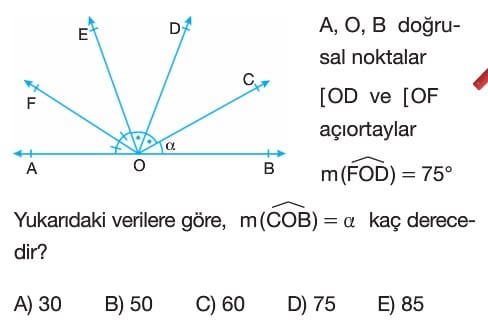
Soru Çözümü
- A, O, B noktaları doğrusal olduğundan, $m(\widehat{AOB}) = 180^\circ$ dir.
- [OD, $\widehat{COE}$ açısının açıortayıdır. Bu nedenle, $m(\widehat{COD}) = m(\widehat{DOE})$ dir. Bu açılara $x$ diyelim. Yani, $m(\widehat{COD}) = m(\widehat{DOE}) = x$.
- [OF, $\widehat{AOE}$ açısının açıortayıdır. Bu nedenle, $m(\widehat{AOF}) = m(\widehat{FOE})$ dir. Bu açılara $y$ diyelim. Yani, $m(\widehat{AOF}) = m(\widehat{FOE}) = y$.
- Verilen bilgiye göre $m(\widehat{FOD}) = 75^\circ$ dir. Şekilde $\widehat{FOD}$ açısı, $\widehat{FOE}$ ve $\widehat{EOD}$ açılarının toplamıdır. Bu durumda, $m(\widehat{FOE}) + m(\widehat{EOD}) = 75^\circ$ olur. Değişkenleri yerine yazarsak, $y + x = 75^\circ$ elde ederiz.
- Doğrusal açı $m(\widehat{AOB})$ tüm küçük açıların toplamıdır: $m(\widehat{AOF}) + m(\widehat{FOE}) + m(\widehat{EOD}) + m(\widehat{DOC}) + m(\widehat{COB}) = 180^\circ$.
- Değişkenleri yerine yazarsak: $y + y + x + x + \alpha = 180^\circ$.
- Bu ifadeyi düzenlersek: $2y + 2x + \alpha = 180^\circ \Rightarrow 2(y + x) + \alpha = 180^\circ$.
- Daha önce bulduğumuz $y + x = 75^\circ$ değerini yerine koyarsak: $2(75^\circ) + \alpha = 180^\circ$.
- $150^\circ + \alpha = 180^\circ$.
- $\alpha = 180^\circ - 150^\circ = 30^\circ$.
- Doğru Seçenek A'dır.