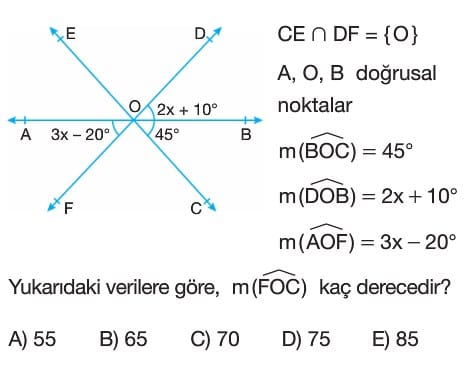
Soru Çözümü
- Verilen bilgilere göre, $\angle AOF$ ve $\angle DOB$ ters açılardır. Ters açıların ölçüleri eşittir.
- Bu nedenle, $m(\angle AOF) = m(\angle DOB)$ denklemini kurarız: `$3x - 20 = 2x + 10$`.
- Denklemi çözerek $x$ değerini buluruz: `$3x - 2x = 10 + 20 \implies x = 30$`.
- Şimdi $m(\angle AOF)$ veya $m(\angle DOB)$ açısının ölçüsünü hesaplayalım: `$m(\angle AOF) = 3(30) - 20 = 90 - 20 = 70^\circ$`. (Veya `$m(\angle DOB) = 2(30) + 10 = 60 + 10 = 70^\circ$`)
- A, O, B noktaları doğrusal olduğu için $\angle AOB$ bir doğru açıdır ($180^\circ$). Bu durumda $\angle AOF$ ve $\angle FOB$ bütünler açılardır.
- $m(\angle AOF) + m(\angle FOB) = 180^\circ$ olduğundan, `$70^\circ + m(\angle FOB) = 180^\circ \implies m(\angle FOB) = 110^\circ$`.
- Şekilden görüldüğü üzere, $\angle FOB$ açısı $\angle FOC$ ve $\angle COB$ açılarının toplamına eşittir: `$m(\angle FOB) = m(\angle FOC) + m(\angle COB)$`.
- Verilen $m(\angle BOC) = 45^\circ$ değerini yerine koyarsak: `$110^\circ = m(\angle FOC) + 45^\circ$`.
- $m(\angle FOC)$ açısının ölçüsünü bulmak için denklemi çözeriz: `$m(\angle FOC) = 110^\circ - 45^\circ = 65^\circ$`.
- Doğru Seçenek B'dır.