Bu yazımızda 9. sınıf matematik müfredatında bulunan Oran ve Orantı konu anlatımı yer almaktadır. Konu anlatımını bitirdikten sonra Oran ve Orantı Soru Çözümleri yazımıza da bakabilirsiniz.

Oran ve Orantı Konu Anlatımı

Oran: En az biri sıfırdan farklı, aynı birimden iki çokluğun bölümüne (karşılaştırılmasına) oran denir. a nın b ye oranı a / b şeklinde gösterilir.

Örneğin;

• Elif 30, Melike 12 yaşında ise Melike’nin yaşının Elif’in yaşına oranı: 12 / 30 = 2 / 5 dir.
• Tuğçe’nin ağırlığı 40 kg, Ebru’nun ağırlığı 60 kg ise Tuğçe’nin ağırlığının, Ebru’nun ağırlığına oranı: 40 kg / 60 kg = 2 / 3 tür.
• 5 kg un ile 2 kg yağ karıştırıldığında un / yağ 5 / 2 oranı olup, elde edilen 7 kg lık karışımın yağ oranı: yağ (kg) / Karışım (Kg) = 2 / 7 dir.

Orantı Çeşitleri

Doğru Orantı: İki çokluktan biri artarken diğeri de aynı oranda artıyorsa veya biri azalırken diğeri de aynı oranda azalıyorsa bu iki çokluk doğru orantılıdır veya kısaca orantılıdır denir.

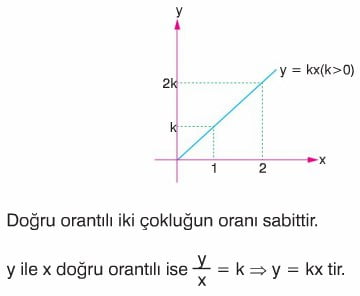
Ters Orantı: İki çokluktan biri artarken diğeri de aynı oranda azalıyorsa ya da biri azalırken diğeri de aynı oranda artıyorsa bu iki çokluk ters orantılıdır denir.

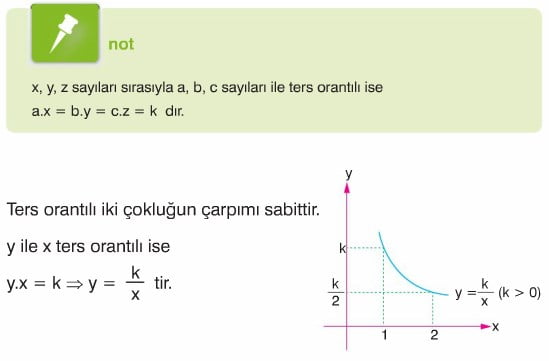
Bileşik Orantı: En az iki doğru veya ters orantıdan oluşan orantılardır.

• y sayısı; x ile doğru, z ile ters orantılı ise y.z/x = k dır.
• Bileşik orantı problemlerinde kapasite, zaman, işçi sayısı gibi değişkenler yapılan iş ile doğru orantılı olduğundan yapılan işin diğer değişkenlerin çarpımına oranı sabittir.

Aritmetik ve Geometrik Ortalama

Değişim Oranı

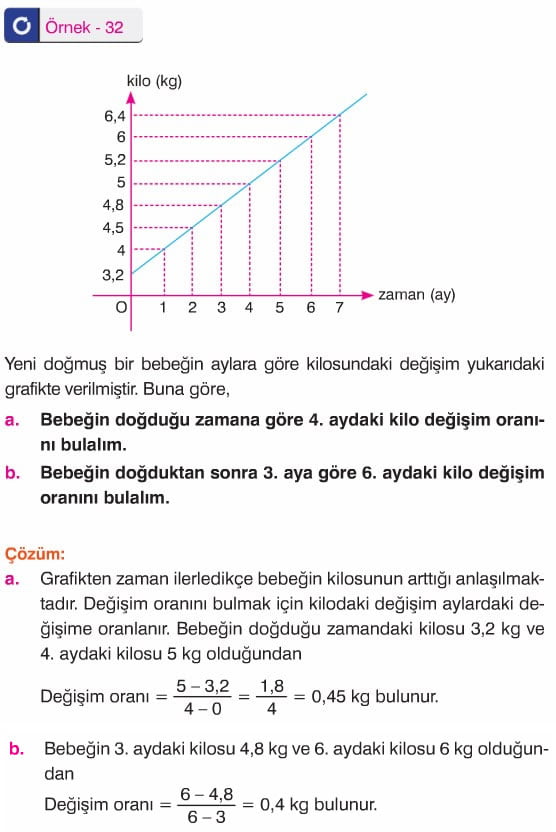
Değişen farklı iki niceliğin karşılaştırılmasıdır. Örneğin, yeni doğmuş bir bebeğin aylara göre kilosu değişir. Kiloda oluşan değişimin zamandaki değişime oranlanmasıyla değişim oranı bulunur.

Ağırlıklı Ortalama

Veriler içerisindeki her bir değerin belirli bir ağırlıkla ayrı ayrı çarpıldıktan sonra bulunan toplamın ağırlık toplamına bölünmesiyle elde edilen ortalamadır. Aşağıdaki örneği inceleyelim.

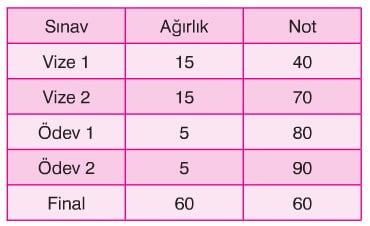
Öğrencinin sınav sonuçları ve bu sınavların ağırlıklarını içeren tablo yukarıda verilmiştir. Öğrencinin bu dersten aldığı genel başarı notu ağırlıklı ortalamaya göre hesaplanır. Eğer sınavların ağırlıkları birbirinden farklı olmasaydı bu dersten genel başarı notu aritmetik ortalama ile
(40+70+80+90+60) / 5 = 68 olacaktır.
Ancak sınavların ağırlıkları farklı olduğundan ağırlıklar ile notların çarpımı yapılarak toplanır. Bu toplam ağırlıklar toplamına bölünür.
Ağırlıklı Ortalama = (40.15+70.15+80.5+90.5+60.60) / 15+15+5+5+60 = 61 bulunur.

Oran ve Orantı Soru Çözümleri

Oran Orantı Ekol Hoca

Çözümlü Örnek Test Soruları

Soru 1
Bir sınıfta 12 erkek ve 8 kız öğrenci bulunmaktadır. Erkek öğrencilerin sayısının, kız öğrencilerin sayısına oranı nedir?

A) 3/2
B) 2/3
C) 3/5
D) 5/3

Çözüm: Erkek öğrencilerin sayısının kız öğrencilerin sayısına oranı 12/8 olur. Sadeleştirildiğinde 3/2 bulunur. Cevap: A

Soru 2
x : y = 4 : 5 oranında ise x ve y toplamı 36 olduğuna göre, x kaçtır?

A) 16
B) 20
C) 24
D) 28

Çözüm: x : y = 4 : 5 oranında olduğuna göre x = 4k ve y = 5k diyebiliriz. x + y = 36 olduğuna göre 4k + 5k = 36’dan 9k = 36, k = 4 bulunur. Bu durumda x = 4 × 4 = 16’dır. Cevap: A

Soru 3
Bir orantıda 6/8 = x/12 olduğuna göre x kaçtır?

A) 9
B) 10
C) 12
D) 14

Çözüm: İçler dışlar çarpımı yaparak 6 × 12 = 8 × x’den x = 9 bulunur. Cevap: A

Soru 4
Bir kutuda 30 mavi, 20 kırmızı ve 10 sarı bilye bulunmaktadır. Mavi bilyelerin toplam bilye sayısına oranı nedir?

A) 1/2
B) 3/5
C) 2/3
D) 1/3

Çözüm: Toplam bilye sayısı 30 + 20 + 10 = 60’tır. Mavi bilyelerin sayısının toplam bilye sayısına oranı 30/60 = 1/2 bulunur. Cevap: A

Soru 5
a : b = 2 : 3 ve b : c = 4 : 5 olduğuna göre, a : c oranı nedir?

A) 8 : 15
B) 2 : 5
C) 5 : 8
D) 3 : 4

Çözüm: a : b = 2 : 3 ve b : c = 4 : 5 oranını kullanarak b’yi eşitlememiz gerekir. İlk oranı 4 ile, ikinci oranı 3 ile genişleterek a : b : c = 8 : 12 : 15 bulunur. Bu durumda a : c = 8 : 15’dir. Cevap: A

Soru 6
Bir havuzda bulunan su miktarı, bir muslukla her saat başı aynı oranda arttırılıyor. İlk saatte 10 litre, ikinci saatte 20 litre, üçüncü saatte 30 litre su eklendiğine göre, bu orantı nasıl tanımlanır?

A) Doğru orantı
B) Ters orantı
C) Sabit oran
D) Oransızlık

Çözüm: Su miktarı saat başı sabit bir oranla artıyorsa, artış doğrusal bir orantıyı gösterir. Bu durumda orantı doğru orantıdır. Cevap: A

Soru 7
x ve y doğru orantılıdır. x = 12 iken y = 16 olduğuna göre, x = 18 iken y kaç olur?

A) 20
B) 22
C) 24
D) 28

Çözüm: Doğru orantı olduğuna göre, x/y sabit bir orandır. x/y = 12/16 = 3/4’tür. x = 18 iken y = (4/3) × 18 = 24 bulunur. Cevap: C