Not: Konunun sonunda diğer hocalar tarafından hazırlanmış köklü ifadeler konu anlatımı videolarını bulabilirsiniz.
Köklü ifadeler




Köklü İfadelerin Özellikleri


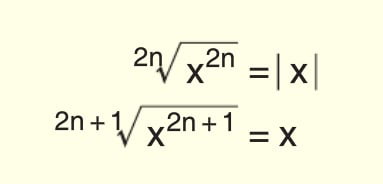
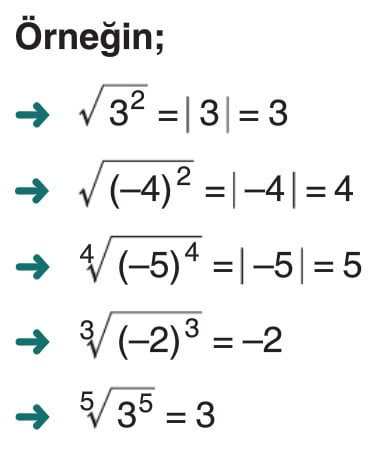

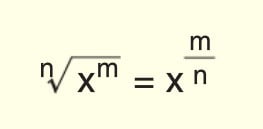
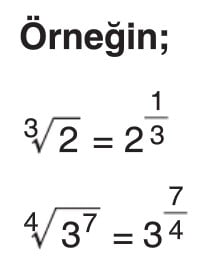


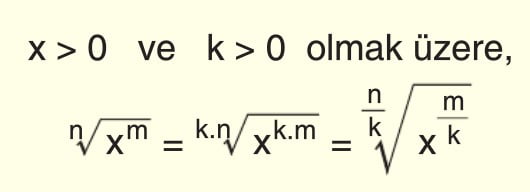
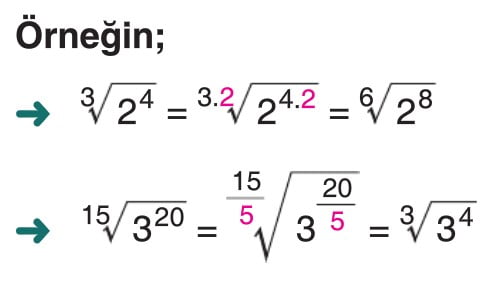



Paydanın Rasyonel Yapılması
Paydasında köklü sayı bulunan bir kesrin paydasını kökten kurtarma işlemine paydanın rasyonel yapılması denir.


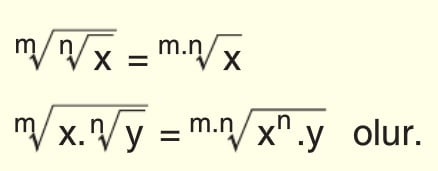
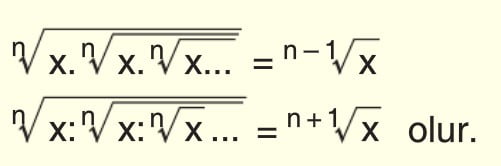








GERÇEKTEN ELİNİZE EMEĞİNİZE SAĞLIK